Squeezed Limits Of Bispectrum Desi: A Concise Guide For Cosmology

Squeezed Limits Of Bispectrum Desi is a focal idea in cosmology that captures how primordial fluctuations couple across scales. This concise guide explains what the squeezed limits of the bispectrum mean, why they matter, and how researchers extract cosmological information from them.

Squeezed Limits Of Bispectrum Desi: Concept and Relevance

Shape Of The Difference Of The Reduced Cross Correlation Bispectrum And

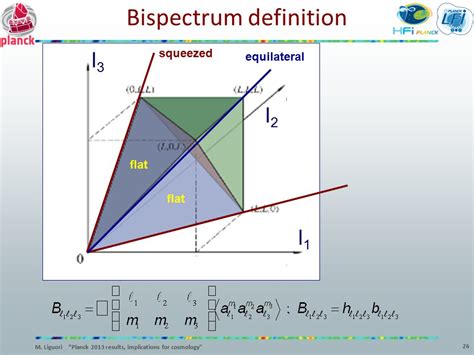
In cosmology, the bispectrum describes three-point correlations in the density field. The squeezed limit refers to configurations where one wavenumber is much smaller than the other two, revealing how large-scale modes modulate small-scale structure. The phrase Squeezed Limits Of Bispectrum Desi is used to signal a focused analysis within the broader bispectrum framework and guides how we interpret non-Gaussian features in the cosmic microwave background and galaxy surveys.

Key Points

The squeezed configuration isolates coupling between long-wavelength and short-wavelength modes, a window into primordial physics.
Templates for the squeezed bispectrum help separate primordial signals from late-time gravitational effects.
Accurate modeling of galaxy bias, redshift-space distortions, and transfer functions is essential in interpreting the squeezed limit.
Survey design, sky coverage, and volume affect the statistical power to detect squeezed-limit signals.
Simulations that resolve a wide dynamic range are crucial for validating theoretical predictions of the squeezed bispectrum.

Theoretical Framework for Squeezed Limits Of Bispectrum Desi

Primordial Non Gaussianity And Bispectrum Measurements In The Cosmic Microwave Background And Large Scale Structure Liguori 2010 Advances In Astronomy Wiley Online Library

The squeezed limit is often analyzed in terms of a consistency relation that links the bispectrum in the squeezed configuration to the derivative of the power spectrum with respect to long-wavelength perturbations. In Squeezed Limits Of Bispectrum Desi analyses, one uses perturbation theory, effective field theory of large-scale structure, and halo models to predict the shape and amplitude of the squeezed signal.

Mathematical form and intuition

In three-point statistics, the bispectrum B(k1,k2,k3) in the squeezed limit k1 ≪ k2 ≈ k3 reveals how a large-scale mode δL modulates the small-scale power. The leading behavior often scales with δL times a response function, linking to primordial non-Gaussianity parameters if present.

Practical Approach to Measuring Squeezed Limits Of Bispectrum Desi

Measuring the squeezed bispectrum requires careful handling of survey geometry, mask effects, and covariance estimation. Analysts construct estimators that optimize sensitivity to the squeezed configuration while mitigating contaminations from systematics.

Data considerations

Data from galaxy redshift surveys, weak lensing maps, and the CMB are all relevant. The squeezed limit is sensitive to large-scale modes, so cosmic variance and survey window functions must be accounted for with accurate mock catalogs.

Applications of Squeezed Limits Of Bispectrum Desi in Observations

Applying squeezed-limit analysis to real data involves comparing measured bispectrum shapes to theoretical templates. This helps reveal whether observed non-Gaussian features arise from early-Universe physics or from late-time processes like gravitational evolution and biasing.

Implications for Cosmological Parameters

An Adaptive Feature Extraction Technique Via Bispectrum Driving Graph Domain For Bearing Fault Diagnosis Sciencedirect

Constraints from the squeezed limits of the bispectrum inform models of inflation, dark energy, and structure growth. By comparing observations with theoretical templates tailored to the Squeezed Limits Of Bispectrum Desi, researchers can tighten bounds on primordial non-Gaussianity and the physics of early-Universe fluctuations.

What exactly are squeezed limits in the bispectrum?

The squeezed limit refers to a bispectrum configuration where one wavevector is much smaller than the other two, highlighting how large-scale fluctuations modulate small-scale structure. It is a powerful probe of how different scales couple in the early universe and in subsequent evolution.

How does Squeezed Limits Of Bispectrum Desi help constrain cosmological parameters?

By matching observed squeezed-limit signals to theoretical templates, researchers can bound primordial non-Gaussianity, test inflationary models, and constrain the growth rate of structure. This adds information beyond what the power spectrum alone provides.

Which surveys are best for studying squeezed-limits signals?

Large-volume galaxy surveys like DESI, Euclid, and LSST are especially powerful for squeezed limits because they cover vast volumes and access many long-wavelength modes. CMB experiments also contribute unique squeezed-limit information through temperature and polarization correlations.

What are the main challenges in modeling squeezed limits?

Key challenges include separating primordial non-Gaussian signals from late-time gravitational evolution, accurately modeling galaxy bias and redshift-space distortions, accounting for survey window functions, and controlling cosmic variance with realistic mocks and simulations.